Considere la cascada de los dos tanques mostrados en la figura 1.5.5, siendo los volúmenes de cada tanque V1= 100 (gal) y V2= 200 (gal) respectivamente.
Aunado a ello, cada tanque contiene inicialmente 50 lb de sal. Las tres tasas
de flujo indicadas en la figura son —cada una— de 5 gal/min, siendo de agua pura el flujo
de entrada al tanque 1.
(a) Encuentre la cantidad x(t) de sal en el tanque 1 en el tiempo t.
(b) Suponga que y(t) es la cantidad de sal del tanque 2 en t. Muestre que
y después resuelva para y(t) aplicando la función x(t) encontrada
en el inciso (a).
(c) Finalmente, halle la
cantidad máxima de sal en el tanque 2.
Resolución
a)
Para deducir la ecuación diferencial que nos permita determinar
la cantidad de sal en cualquier instante, nos concentraremos en un pequeño intervalo de tiempo, por ejemplo, ( t , t+ ∆t) , y razonaremos lo que ocurre con la cantidad sal en el tanque 1.
En ese tiempo, ∆t, existirá una pequeña variación en la cantidad de sal, que es la siguiente:
¿Cuánta sal entra al estanque en
∆t min?
Entran cero gramos, dado que
solo está entrando agua pura, es decir:
Grms de entrada= Flujo de
agua * concentración de soluto (sal)*∆t
Grms de entrada= 5gal/min * 0*∆t=0
¿Cuánta sal sale del estanque en ∆t min?
Grms de salida= Flujo de agua * concentración de
soluto (sal)*∆t
Entonces tenemos que:
b)
En esencia el razonamiento es el mismo usado en a)
q0: Es el caudal de entrada al tanque 2
q1: Es el caudal de salida del
tanque 2
c0: Es la concentración
de soluto en el caudal de entrada al tanque2
c1: Es la concentración de soluto en el
caudal de salida del tanque2
Comentario: Dado que el caudal de entrada es igual al caudal de
salida, el volumen en cada estanque es constante en el tiempo.
Hemos demostrado lo solicitado.
Ahora resolveremos
esta ecuación diferencial, para ello empezaremos reemplazando x por el valor obtenido
en a):
Escribimos la ecuación en la forma:
Para resolver esta Ecuación
Lineal de Primer Orden seguiremos los siguientes pasos:
1.- Calcular factor de integración:
2.- Multiplicar ambos lados de la ecuación (2) por el factor de integración
ρ(t):
3.- El lado izquierdo de la ecuación (3) identificarlo como la
derivada de un producto:
4.- Integrar la ecuación (4)
c)
Cantidad máxima de sal en el
estanque 2
La cantidad máxima de sal en el estanque 2 se
producirá en el minuto en que la pendiente de y(t) sea cero, es decir, y’(t)=0


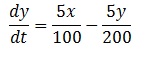













Increible, Gracias!
ResponderEliminarmuy bueno, gracias
ResponderEliminarMuy bueno que amable al compartir tal información
ResponderEliminar