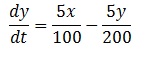8.- Aplicación Ley de Torricelli

8. Un tanque de agua tiene la forma obtenida al girar la parábola x² alrededor del eje y. La profundidad del agua es de 4 ft a las 12 del día, cuando se quita el tapón circular del fondo del tanque. A la 1 P.M. la profundidad del agua es de 1 ft.

(a) ¿Cuál es la profundidad del agua y(t) que permanece después de t h?

(b) ¿Cuándo queda vacío el tanque?

(c) Si el radio inicial de la superficie superior del agua es de 2 ft, ¿cuál es el radio del orificio circular en el fondo?

DESARROLLO

Para resolver este problema aplicaremos la Ley de Torricelli:

7.- Aplicación Ecuaciones Diferenciales de primer orden: Tanques en cascada con etanol

Suponga que en la cascada mostrada en la figura 1.5.5 inicialmente el tanque 1 contiene 100 gal de etanol puro y el tanque 2 contiene 100 gal de agua pura. El flujo de entrada al tanque 1 es de 10 gal/min de agua pura, y los otros dos flujos son también de 10 gal/min.

 (a) Encuentre las cantidades x(t) y y(t) de etanol en los dos tanques en el tiempo t≥0.

 (b) Descubra la cantidad máxima de etanol en el tanque 2

6. Aplicación Ecuaciones Diferenciales de primer orden: Dos tanques en cascada

Considere la cascada de los dos tanques mostrados en la figura  1.5.5, siendo los volúmenes de cada tanque V₁=  100 (gal) y V₂=  200 (gal) respectivamente. Aunado a ello, cada tanque contiene inicialmente 50 lb de sal. Las tres tasas de flujo indicadas en la figura son —cada una— de 5 gal/min, siendo de agua pura el flujo de entrada al tanque 1.

(a) Encuentre la cantidad x(t) de sal en el tanque 1 en el tiempo t.

(b) Suponga que y(t) es la cantidad de sal del tanque 2 en t. Muestre que

y después resuelva para y(t) aplicando la función x(t) encontrada en el inciso (a).

(c) Finalmente, halle la cantidad máxima de sal en el tanque 2.

Aviso

Estimados visitantes,

Agradezco vuestra acogida. También pido las disculpas del caso por haber dejado de subir problemas resueltos de ecuaciones diferenciales.

A partir del 15 de julio y hasta el 30 julio, resolveré y publicaré todos los  problemas que más pueda.

Atte.

Hugo Marínez L.

Ecuaciones diferenciales: El problema de la braquistócrona

5. La figura 1.4.11 muestra una cuenta deslizándose hacia abajo en un cuerda sin fricción del punto P al punto Q. El  problema de la braquistócrona  pregunta qué forma debe  tener la cuerda a fin de minimizar el tiempo de deslizamiento para descender de P a Q. En junio de 1696, John Bernoulli propuso este problema como un reto para la comunidad científica, ofreciendo un plazo de seis meses (más tarde extendido a la Pascua de 1697 a petición de

George Leibniz). Isaac Newton, entonces retirado de la vida académica y sirviendo como alcalde de la Casa de Moneda en Londres, asumió el reto de Bernoulli el 29 de enero de 1697. Al día siguiente comunicó su solución —la curva de descenso en el tiempo mínimo es un arco de cicloide invertida— a la Real Sociedad de Londres. Para una deducción moderna de este resultado, suponga que la cuenta inicia desde el reposo en el origen P y que y= y(x) es la ecuación de la curva deseada en un sistema de coordenadas con los puntos del eje y hacia abajo. Entonces, una analogía mecánica de la ley de Snell en óptica implica que:

Aplicación Ley de Torricelli: Tanque esférico:

4.- Un tanque esférico con un radio de 4 ft está lleno de gasolina cuando se abre un orificio con un radio de 1 pulgada en la parte inferior, ¿cuánto tiempo se requerirá para que toda la gasolina salga del tanque?

Resolución:

 Bosquejo:

Representamos el radio en función de y, en cualquier sección horizontal del tanque. Por  Pitágoras tenemos que:

Aplicaciones Ecuaciones Diferenciales: La clepsydra, o reloj de agua

2.- (La clepsydra, o reloj de agua) Un reloj de agua de 12 horas se diseña con las dimensiones que se muestran en la figura1.4.10, dada la forma de la superficie obtenida al girar la curva y =f(x)  alrededor del eje y. ¿Cuál debe ser esta curva, y qué radio debe tener el orificio circular del fondo para que el nivel del agua caiga a una velocidad constante de 4 pulgadas por hora in/h?

Resolución:

Impacto de una granada

3.- Se lanza una granada desde un helicóptero suspendido a una altura de 800 ft arriba del piso. Desde el piso, directamente bajo el helicóptero, se dispara un proyectil en línea recta hacia la granada, exactamente 2 s después de que ésta fue soltada. ¿Con qué velocidad inicial debe dispararse el proyectil para que alcance la granada a una altitud de exactamente 400 ft?

Bosquejo:

Bosquejo

Razonamiento:
 1- Se utilizará la la función posición de un cuerpo con moviemiento rectilineo
 2.-Sea y(t) la posicion de la granda mientras desciende, entoces igualasmos y(t)=-400 feet para determinar el tiempo que tarda en descender la granda a los 400feet, llamemos ese tiempo t1.
 3.- Tenemos que en t1-2 el proyectil debe impactar la granda a 400feet de altura.
4.- Sea h(t) la altura del proyectil en cual cualquier momento , entoces h(t1-2)= 400
5.- De la ecuación anterior se despeja la velocidad inicial del proyectil


Click en las imágenes que siguen para ampliar solución

Aplicaciones Ecuaciones Diferenciales: Ley de enfriamiento de Newton

A que horá murió: Ley de enfriamiento de Newton

1.- Justo antes del mediodía se encuentra el cuerpo de una víctima de un presunto homicidio dentro de un cuarto que se conserva a una temperatura constante de 70 °F. A las 12 del día la temperatura del cuerpo es de 80 °F y a la 1 P.M. de 75 °F. Considere que la temperatura del cuerpo al morir era de 98.6 °F y que éste se ha enfriado de acuerdo con la ley de Newton. ¿A qué hora murió la víctima?

Resolución: ( Al final con maple 15)



Nota: Ahora ne se olvide ayudarme haciendo click en la publicidad que está al final del cuadro de comentarios