1.- Calcular las áreas de
los dodecágonos regulares inscrito y circunscrito en un disco circular unidad y deducir del resultado las desigualdades 3 <π
< 12(2 - √3).
- Calculamos el área de dodecágono ( A=3r2 ) , pero loa reamos plaicando la integral.
Al ver la figura de arriba podemos deducir r que su área esta formada por 12 triángulos iguales, por lo tanto calcularemos el área de dicho triangulo y lo multiplicaremos por 12.
Al ver la figura de arriba podemos deducir r que su área esta formada por 12 triángulos iguales, por lo tanto calcularemos el área de dicho triangulo y lo multiplicaremos por 12.
Para ellos determinaremos las ecuaciones
de las rectas que lo forman e integraremos convenientemente.
Las ecuaciones son :
Figura 2
Observación: El punto X1=√3/2 (ver grafico 1) lo calculamos: cos(30°)=X1/1, Y2 de forma similar usando seno.
Area del triángulo:
Area dodecágono inscrito en la circunsferencia unidad= 12*(1/4)= 3
Area de la circunferencia unidad:
Está pendiente por demostrar π< 12(2 - √3),
dónde 12(2 - √3) es el área del dodecágono circunscrito a la circunferencia de radio 1. Para que
el dodecágono este circunscrito a la circunferencia su apotema debe ser 1. Que es la altura del tríangulo de la figura 3
Dodecágono circunscrito a la circunsferencia de radio 1
Dodecágono circunscrito a la circunsferencia de radio 1
Figura 3
Para calcular su área, calculamos el área del triángulo y lo multiplicamos por 12, dado por las ecuaciones:
Para determinar las ecuaciones debemos calcular la distancia
r, a y b.
Nota: recordar que apotema=1
Ecuaciones que reppesentan el triangulo:
AREA DODECAGONO CIRCUSNCRITO:
Por lo tanto se cumple: 3 <π< 12(2 - √3).





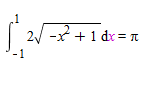




No hay comentarios:
Publicar un comentario